home · about · projects

Image from Wikimedia Commons

Classifying the Iris Data Set with PyTorch

27 Sep 2020

Table of Contents

In this short article we will have a look on how to use PyTorch with the Iris data set. We will create and train a neural network with Linear layers and we will employ a Softmax activation function and the Adam optimizer.

Data Preperation

To prepare the data, we will use a StandardScaler to remove the mean and scale the features to unit variance. Finally we want to perform a train test split to compare our results later on.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

plt.style.use('ggplot')

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

iris = load_iris()
X = iris['data']
y = iris['target']
names = iris['target_names']
feature_names = iris['feature_names']

# Scale data to have mean 0 and variance 1 
# which is importance for convergence of the neural network
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# Split the data set into training and testing
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=2)

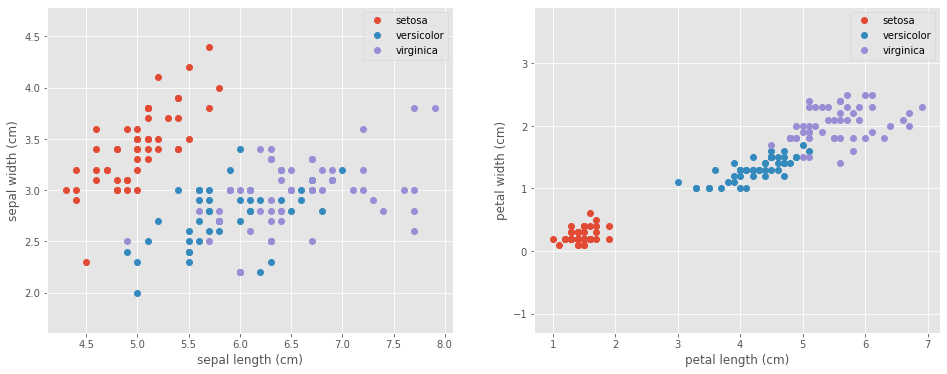
Visualize the Data

Let’s take a look at our data to see what we are dealing with.

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
for target, target_name in enumerate(names):
    X_plot = X[y == target]
    ax1.plot(X_plot[:, 0], X_plot[:, 1], 
             linestyle='none', 
             marker='o', 
             label=target_name)
ax1.set_xlabel(feature_names[0])
ax1.set_ylabel(feature_names[1])
ax1.axis('equal')
ax1.legend();

for target, target_name in enumerate(names):
    X_plot = X[y == target]
    ax2.plot(X_plot[:, 2], X_plot[:, 3], 
             linestyle='none', 
             marker='o', 
             label=target_name)
ax2.set_xlabel(feature_names[2])
ax2.set_ylabel(feature_names[3])
ax2.axis('equal')
ax2.legend();

png

Configure Neural Network Models

import torch
import torch.nn.functional as F
import torch.nn as nn
from torch.autograd import Variable

class Model(nn.Module):
    def __init__(self, input_dim):
        super(Model, self).__init__()
        self.layer1 = nn.Linear(input_dim, 50)
        self.layer2 = nn.Linear(50, 50)
        self.layer3 = nn.Linear(50, 3)
        
    def forward(self, x):
        x = F.relu(self.layer1(x))
        x = F.relu(self.layer2(x))
        x = F.softmax(self.layer3(x), dim=1)
        return x

model     = Model(X_train.shape[1])
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
loss_fn   = nn.CrossEntropyLoss()
model

Model(
  (layer1): Linear(in_features=4, out_features=50, bias=True)
  (layer2): Linear(in_features=50, out_features=50, bias=True)
  (layer3): Linear(in_features=50, out_features=3, bias=True)
)

Train the Model

Now its time to run the training. In order to track progress more efficiently, we can use tqdm, which is a great and easy to use progress bar for our training epochs.

import tqdm

EPOCHS  = 100
X_train = Variable(torch.from_numpy(X_train)).float()
y_train = Variable(torch.from_numpy(y_train)).long()
X_test  = Variable(torch.from_numpy(X_test)).float()
y_test  = Variable(torch.from_numpy(y_test)).long()

loss_list     = np.zeros((EPOCHS,))
accuracy_list = np.zeros((EPOCHS,))

for epoch in tqdm.trange(EPOCHS):
    y_pred = model(X_train)
    loss = loss_fn(y_pred, y_train)
    loss_list[epoch] = loss.item()
    
    # Zero gradients
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    
    with torch.no_grad():
        y_pred = model(X_test)
        correct = (torch.argmax(y_pred, dim=1) == y_test).type(torch.FloatTensor)
        accuracy_list[epoch] = correct.mean()

100%|██████████| 100/100 [00:00<00:00, 407.99it/s]

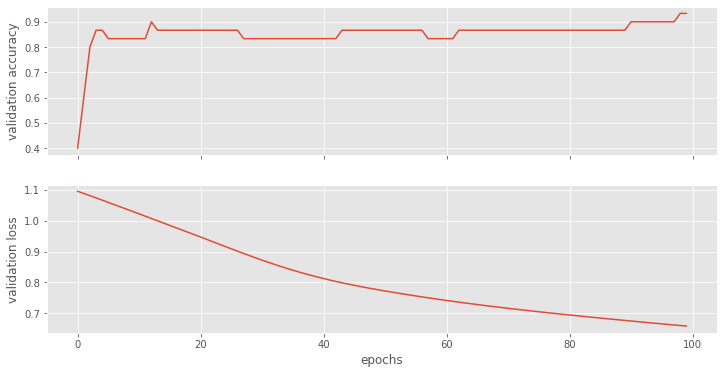
Plot Accuracy and Loss from Training

Let’s have a look how our models perform. We can clearly see that adding more nodes makes the training perform better.

fig, (ax1, ax2) = plt.subplots(2, figsize=(12, 6), sharex=True)

ax1.plot(accuracy_list)
ax1.set_ylabel("validation accuracy")
ax2.plot(loss_list)
ax2.set_ylabel("validation loss")
ax2.set_xlabel("epochs");

png

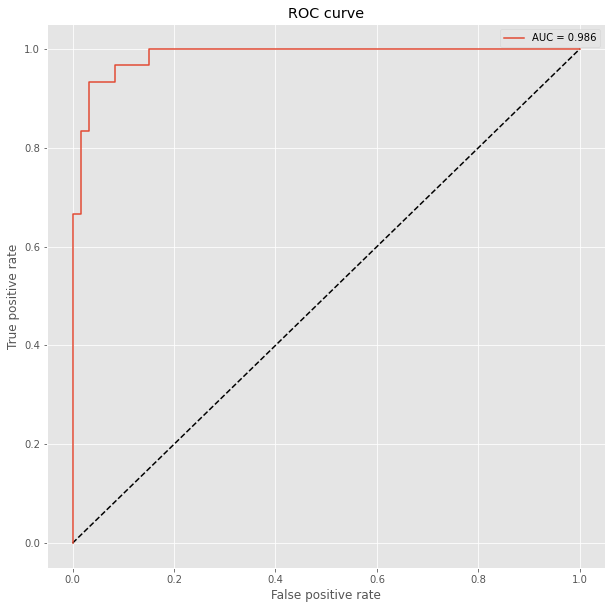
Show ROC Curve

We have previously split the data and we can compare now with the Receiver Operating Characteristic (ROC) how well the models perform. The ROC plot compares the false positive rate with the true positive rate. We additionally compute for each model the Area under the curve (AUC), where auc = 1 is perfect classification and auc = 0.5 is random guessing (for a two class problem). To prepare the test data, we need to use the OneHotEncoder to encode the integer features into a One-hot vector which we then flatten with numpy.ravel() for sklearn.metrics.roc_curve().

from sklearn.metrics import roc_curve, auc
from sklearn.preprocessing import OneHotEncoder

plt.figure(figsize=(10, 10))
plt.plot([0, 1], [0, 1], 'k--')

# One hot encoding
enc = OneHotEncoder()
Y_onehot = enc.fit_transform(y_test[:, np.newaxis]).toarray()

with torch.no_grad():
    y_pred = model(X_test).numpy()
    fpr, tpr, threshold = roc_curve(Y_onehot.ravel(), y_pred.ravel())
    
plt.plot(fpr, tpr, label='AUC = {:.3f}'.format(auc(fpr, tpr)))
plt.xlabel('False positive rate')
plt.ylabel('True positive rate')
plt.title('ROC curve')
plt.legend();

png

Related Posts